library(knitr)
## Warning: package 'knitr' was built under R version 3.0.3
opts_knit$set(global.par=TRUE)
opts_chunk$set(cache.extra = rand_seed,fig.align='center')
set.seed(23)
The general idea
General ideas of linear regression is that
- Response is continous, theoretically from -infinity to + infinity
- Residuals are normally distributed around the model predictions
Idea of the GLM framework is take the linear regression framework, but allow relaxing both assumptions. To do this, we have to do two things
- We wrap the linear model in a transformation function that forces the response on the right interval (typical intervals are positive, or between 0 and 1). This transformation is called the link function
- We use other distributions as the Gaussian for the fit.
Those two ideas are explained in more detail below
Other distributions
Link function
Important GLM types
Logistic Regression
Presence / absence data - binary data Logistic regression is a method for fitting a regression curve, y = f(x), when y consists of proportions or probabilities, or binary coded (0,1–failure,success) data. When the response is a binary (dichotomous) variable, and x is numerical, logistic regression fits a logistic curve to the relationship between x and y.
Assumptions: The true conditional probabilities are a logistic function of the independent variables. No important variables are omitted. No extraneous variables are included. The independent variables are measured without error. The observations are independent. The independent variables are not linear combinations of each other.
Example 1 - Logistic regresion
Binomial data
require(effects) # holds the data
## Loading required package: effects
## Warning: package 'effects' was built under R version 3.0.3
head(TitanicSurvival)
## survived sex age passengerClass
## Allen, Miss. Elisabeth Walton yes female 29.0000 1st
## Allison, Master. Hudson Trevor yes male 0.9167 1st
## Allison, Miss. Helen Loraine no female 2.0000 1st
## Allison, Mr. Hudson Joshua Crei no male 30.0000 1st
## Allison, Mrs. Hudson J C (Bessi no female 25.0000 1st
## Anderson, Mr. Harry yes male 48.0000 1st
attach(TitanicSurvival)
plot(survived ~ age)

surv <- as.numeric(survived)-1
plot(surv ~ age)

fmt <- glm(surv ~ age + I(age^2) + I(age^3), family=binomial)
summary(fmt)
##
## Call:
## glm(formula = surv ~ age + I(age^2) + I(age^3), family = binomial)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.506 -0.998 -0.970 1.348 2.014
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 7.85e-01 3.03e-01 2.59 0.0095 **
## age -1.19e-01 3.29e-02 -3.61 0.0003 ***
## I(age^2) 3.41e-03 1.11e-03 3.07 0.0022 **
## I(age^3) -2.93e-05 1.11e-05 -2.65 0.0081 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 1414.6 on 1045 degrees of freedom
## Residual deviance: 1398.5 on 1042 degrees of freedom
## (263 observations deleted due to missingness)
## AIC: 1406
##
## Number of Fisher Scoring iterations: 4
Showing that residuals are not normal at all
hist(fmt$residuals, breaks = 100)
abline(v = 0, col = "red", lwd = 6, lty = 2)
residual plots can also be created with plot(fmt)
newage <- seq(min(age, na.rm=T), max(age, na.rm=T), len=100)
preds <- predict(fmt, newdata=data.frame("age"=newage), se.fit=T)
lines(newage, plogis(preds$fit), col="purple", lwd=3)
lines(newage, plogis(preds$fit-2*preds$se.fit), col="purple", lwd=3, lty=2)
lines(newage, plogis(preds$fit+2*preds$se.fit), col="purple", lwd=3, lty=2)

fmt <- glm(surv ~ age + sex + passengerClass, family=binomial)
summary(fmt)
##
## Call:
## glm(formula = surv ~ age + sex + passengerClass, family = binomial)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.640 -0.698 -0.434 0.669 2.396
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 3.52207 0.32670 10.78 < 2e-16 ***
## age -0.03439 0.00633 -5.43 5.6e-08 ***
## sexmale -2.49784 0.16604 -15.04 < 2e-16 ***
## passengerClass2nd -1.28057 0.22554 -5.68 1.4e-08 ***
## passengerClass3rd -2.28966 0.22580 -10.14 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 1414.62 on 1045 degrees of freedom
## Residual deviance: 982.45 on 1041 degrees of freedom
## (263 observations deleted due to missingness)
## AIC: 992.5
##
## Number of Fisher Scoring iterations: 4
detach(TitanicSurvival)
Example 2 - Logistic regresion
Wild boar with/without tubercolosis as a function of body lenght (age is collinear with length)
Boar <- read.delim("Z:/GitHub/RMarkdowns - Stat with R/10_GLM binomial/Boar.txt")
Boar <- Boar[!(is.na(Boar$LengthCT)) & !(is.na(Boar$Tb)),]
head(Boar)
## Tb SEX AgeClass LengthCT
## 1 0 1 1 46.5
## 2 0 2 1 47.0
## 3 0 1 1 48.0
## 4 0 1 1 51.5
## 5 0 2 1 53.0
## 6 0 2 1 53.0
summary(Boar)
## Tb SEX AgeClass LengthCT
## Min. :0.000 Min. :1.00 Min. :1.00 Min. : 46.5
## 1st Qu.:0.000 1st Qu.:1.00 1st Qu.:3.00 1st Qu.:106.5
## Median :0.000 Median :2.00 Median :3.00 Median :121.5
## Mean :0.459 Mean :1.58 Mean :3.13 Mean :117.0
## 3rd Qu.:1.000 3rd Qu.:2.00 3rd Qu.:4.00 3rd Qu.:130.0
## Max. :1.000 Max. :2.00 Max. :4.00 Max. :165.0
## NA's :14
cor(Boar[,c(3,4)], use="pairwise.complete.obs")
## AgeClass LengthCT
## AgeClass 1.000 0.891
## LengthCT 0.891 1.000
Data exploration
attach(Boar)
boxplot(LengthCT~Tb,ylab='body length',xlab='Tb')

plot(x=Boar$LengthCT, y = Boar$Tb,xlab="Length", ylab="Tb")
B0=lm(Tb ~LengthCT, data = Boar)
abline(B0)
 The wrong model, as we are working with probabilities, while linear regression also predicts negative probabilities and it is not possible a negative probability of getting sick
The wrong model, as we are working with probabilities, while linear regression also predicts negative probabilities and it is not possible a negative probability of getting sick
We need a function that maps the values between 0 and 1 (e.g., logit link, probit link, clog-log link, log-log link). The default is logit link
B1=glm(Tb ~LengthCT, family = binomial, data = Boar) # logit link is the default
summary(B1)
##
## Call:
## glm(formula = Tb ~ LengthCT, family = binomial, data = Boar)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.609 -1.120 -0.709 1.126 1.952
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -3.89211 0.67115 -5.80 6.7e-09 ***
## LengthCT 0.03161 0.00559 5.66 1.5e-08 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 700.76 on 507 degrees of freedom
## Residual deviance: 663.56 on 506 degrees of freedom
## AIC: 667.6
##
## Number of Fisher Scoring iterations: 4
Probability that an animal is infected is: p=(e^(-3.89+0.03length))/ (1 + e^( -3.89+0.03length))
plot(x=Boar$LengthCT, y = Boar$Tb,xlab="Length", ylab="Tb")
MyData=data.frame(LengthCT= seq(from = 46.5, to =165, by = 1))
Pred<- predict(B1,newdata = MyData, type = "response")
lines(MyData$LengthCT,Pred,col=2,lty=2)

Alternatively
plot.new()
curve(predict(B1,data.frame(LengthCT=x),type="resp"),add=TRUE,col=3)

or we can use the “popbio” package
library(popbio)
## Loading required package: quadprog
logi.hist.plot(LengthCT,Tb,boxp=FALSE,type="hist",col="gray")

another option is to use a GLM
B1.A=glm(Tb ~LengthCT, family = binomial(link="probit"), data = Boar)
summary(B1.A)
##
## Call:
## glm(formula = Tb ~ LengthCT, family = binomial(link = "probit"),
## data = Boar)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.606 -1.122 -0.709 1.127 1.971
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -2.37915 0.39528 -6.02 1.8e-09 ***
## LengthCT 0.01932 0.00331 5.85 5.0e-09 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 700.76 on 507 degrees of freedom
## Residual deviance: 663.58 on 506 degrees of freedom
## AIC: 667.6
##
## Number of Fisher Scoring iterations: 4
logit and probit links assume that there are about the same number of zeros and ones clog-log is a good option if there are a lots of zeros, or viceversa family = binomial(link=”cloglog”)
plot(x=Boar$LengthCT, y = Boar$Tb,xlab="Length", ylab="Tb")
MyData=data.frame(LengthCT= seq(from = 46.5, to =165, by = 1))
Pred<- predict(B1.A,newdata = MyData, type = "response")
lines(MyData$LengthCT,Pred,col=2,lty=2)

Pseudo R Square
#Null Deviance - residual Deviance / Null Deviance
((B1.A$null.deviance-B1.A$deviance)/B1.A$null.deviance)*100 #5% of total variability explained
## [1] 5.307
Example 3 - Logistic regresion
Parasites in cod (fish)
ParasiteCod <- read.delim("Z:/GitHub/RMarkdowns - Stat with R/10_GLM binomial/ParasiteCod.txt")
head(ParasiteCod)
## Sample Intensity Prevalence Year Depth Weight Length Sex Stage Age Area
## 1 1 0 0 1999 220 148 26 0 0 0 2
## 2 2 0 0 1999 220 144 26 0 0 0 2
## 3 3 0 0 1999 220 146 27 0 0 0 2
## 4 4 0 0 1999 220 138 26 0 0 0 2
## 5 5 0 0 1999 220 40 17 0 0 0 2
## 6 6 0 0 1999 220 68 20 0 0 0 2
Response variable: Prevalance 0 1 Explanatories: year, area, depth at which the fishes were caught Depth and area are collinear; other explanatories are sex, length, weight, stage, age..all collinear except for sex
ParasiteCod$fArea = factor(ParasiteCod$Area)
attach(ParasiteCod)
P1 = glm(Prevalence ~ fArea + Length,
family = binomial, data = ParasiteCod)
summary(P1)
##
## Call:
## glm(formula = Prevalence ~ fArea + Length, family = binomial,
## data = ParasiteCod)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.815 -0.970 -0.835 1.157 1.629
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -0.47695 0.26307 -1.81 0.0698 .
## fArea2 -0.70834 0.18143 -3.90 9.5e-05 ***
## fArea3 -0.57601 0.15922 -3.62 0.0003 ***
## fArea4 1.07060 0.17839 6.00 2.0e-09 ***
## Length 0.00874 0.00434 2.01 0.0441 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 1727.8 on 1247 degrees of freedom
## Residual deviance: 1592.0 on 1243 degrees of freedom
## (6 observations deleted due to missingness)
## AIC: 1602
##
## Number of Fisher Scoring iterations: 4
plot(Length,Prevalence)
MyData=data.frame(Length= seq(from = 20, to =100, by = 1),fArea="1")
Pred<- predict(P1,newdata = MyData, type = "response")
lines(MyData$Length,Pred,col=1,lty=1)
MyData=data.frame(Length= seq(from = 20, to =100, by = 1),fArea="2")
Pred<- predict(P1,newdata = MyData, type = "response")
lines(MyData$Length,Pred,col=2,lty=2)
MyData=data.frame(Length= seq(from = 20, to =100, by = 1),fArea="3")
Pred<- predict(P1,newdata = MyData, type = "response")
lines(MyData$Length,Pred,col=3,lty=3)
MyData=data.frame(Length= seq(from = 20, to =100, by = 1),fArea="4")
Pred<- predict(P1,newdata = MyData, type = "response")
lines(MyData$Length,Pred,col=4,lty=4)

A much handier way
plot.new()
curve(predict(P1,data.frame(Length=x,fArea="1"),type="resp"),add=TRUE,col=1,lwd=2)
curve(predict(P1,data.frame(Length=x,fArea="2"),type="resp"),add=TRUE,col=2,lwd=2)
curve(predict(P1,data.frame(Length=x,fArea="3"),type="resp"),add=TRUE,col=3,lwd=2)
curve(predict(P1,data.frame(Length=x,fArea="4"),type="resp"),add=TRUE,col=4,lwd=2)

Example 4 - Logistic regresion
Tubercolosis in deer, this time proportion data (ranging from 0 to 1)
Tbdeer <- read.delim("Z:/GitHub/RMarkdowns - Stat with R/10_GLM binomial/Tbdeer.txt")
head(Tbdeer)
## Farm BoarPosTB BoarSampledTB DeerPosTB DeerSampledTB DeerPosCervi
## 1 1 4 14 NA NA NA
## 2 2 20 34 3 13 6
## 3 3 2 5 0 23 28
## 4 4 8 13 1 39 39
## 5 5 7 23 0 6 13
## 6 6 11 20 2 36 19
## DeerSampledCervi OpenLand ScrubLand PinePlantation QuercusPlants
## 1 NA 0.409 0.591 0.000 7.000
## 2 15 0.412 0.059 0.000 14.706
## 3 28 0.182 0.136 0.091 5.318
## 4 45 0.300 0.250 0.000 14.737
## 5 13 0.000 0.571 0.000 9.333
## 6 25 0.286 0.476 0.000 21.543
## QuercusTrees WildBoarIndex ReedDeerIndex EstateSize Fenced
## 1 1.619 0.095 0.000 960 0
## 2 0.118 0.576 17.470 1100 1
## 3 4.045 0.450 19.412 2200 1
## 4 4.200 0.100 6.318 1700 1
## 5 0.952 0.000 4.364 4000 0
## 6 2.972 0.238 5.141 19328 0
Tbdeer$DeerPosProp = Tbdeer$DeerPosCervi / Tbdeer$DeerSampledCervi # proportion of deer infected
Tbdeer$fFenced = factor(Tbdeer$Fenced)
Effect of percentage open land, scrubs, pine plantation, number of quercus per unit area, red deer abundance index, estate size, estate fenced ON probability of getting infected
Deer2 <- glm(DeerPosProp~OpenLand+ScrubLand+ReedDeerIndex+
fFenced,
family=binomial,weights=DeerSampledCervi,data = Tbdeer)
summary(Deer2)
##
## Call:
## glm(formula = DeerPosProp ~ OpenLand + ScrubLand + ReedDeerIndex +
## fFenced, family = binomial, data = Tbdeer, weights = DeerSampledCervi)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -8.652 -0.827 0.560 2.057 3.877
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 2.3635 0.3608 6.55 5.7e-11 ***
## OpenLand -3.3056 0.5493 -6.02 1.8e-09 ***
## ScrubLand -0.7810 0.5271 -1.48 0.1384
## ReedDeerIndex 0.0629 0.0203 3.11 0.0019 **
## fFenced1 -1.1491 0.3582 -3.21 0.0013 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 235.58 on 23 degrees of freedom
## Residual deviance: 164.83 on 19 degrees of freedom
## (8 observations deleted due to missingness)
## AIC: 233.9
##
## Number of Fisher Scoring iterations: 4
This is a Binomial GLM with proportion data. We can have overdispersion. Residual deviance / df should be ~1
Deer2$deviance / Deer2$df.residual #~9
## [1] 8.675
library(effects)
plot(allEffects(Deer2))

We add a dispersion parameter to the variance of Y
Deer3 <- glm(DeerPosProp~OpenLand+ScrubLand+ReedDeerIndex+
fFenced,
family=quasibinomial,weights=DeerSampledCervi,data = Tbdeer)
summary(Deer3)
##
## Call:
## glm(formula = DeerPosProp ~ OpenLand + ScrubLand + ReedDeerIndex +
## fFenced, family = quasibinomial, data = Tbdeer, weights = DeerSampledCervi)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -8.652 -0.827 0.560 2.057 3.877
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.3635 1.1133 2.12 0.047 *
## OpenLand -3.3056 1.6949 -1.95 0.066 .
## ScrubLand -0.7810 1.6262 -0.48 0.637
## ReedDeerIndex 0.0629 0.0625 1.01 0.327
## fFenced1 -1.1491 1.1051 -1.04 0.311
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for quasibinomial family taken to be 9.52)
##
## Null deviance: 235.58 on 23 degrees of freedom
## Residual deviance: 164.83 on 19 degrees of freedom
## (8 observations deleted due to missingness)
## AIC: NA
##
## Number of Fisher Scoring iterations: 4
Deer3$deviance / Deer3$df.residual
## [1] 8.675
plot(allEffects(Deer3))
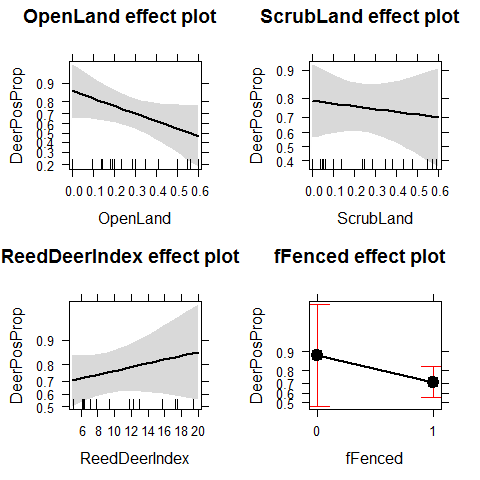
We have lost many of the significant patters that were biased by overdispersion. The new results look pretty different
plot(Tbdeer$OpenLand,Tbdeer$DeerPosProp)
curve(predict(Deer3,data.frame(OpenLand=x, # scenario "no fenced"
ScrubLand=mean(Tbdeer$ScrubLand),
ReedDeerIndex=mean(Tbdeer$ReedDeerIndex),
fFenced="0"),type="resp"),add=TRUE,col=1,lwd=2)
curve(predict(Deer3,data.frame(OpenLand=x, # scenario "fenced"
ScrubLand=mean(Tbdeer$ScrubLand),
ReedDeerIndex=mean(Tbdeer$ReedDeerIndex),
fFenced="1"),type="resp"),add=TRUE,col=2,lwd=2)

Plotting predictions with 95% CIs
Boar <- read.delim("Z:/GitHub/RMarkdowns - Stat with R/10_GLM binomial/Boar.txt")
Boar <- Boar[!(is.na(Boar$LengthCT)) & !(is.na(Boar$Tb)),]
head(Boar)
## Tb SEX AgeClass LengthCT
## 1 0 1 1 46.5
## 2 0 2 1 47.0
## 3 0 1 1 48.0
## 4 0 1 1 51.5
## 5 0 2 1 53.0
## 6 0 2 1 53.0
summary(Boar)
## Tb SEX AgeClass LengthCT
## Min. :0.000 Min. :1.00 Min. :1.00 Min. : 46.5
## 1st Qu.:0.000 1st Qu.:1.00 1st Qu.:3.00 1st Qu.:106.5
## Median :0.000 Median :2.00 Median :3.00 Median :121.5
## Mean :0.459 Mean :1.58 Mean :3.13 Mean :117.0
## 3rd Qu.:1.000 3rd Qu.:2.00 3rd Qu.:4.00 3rd Qu.:130.0
## Max. :1.000 Max. :2.00 Max. :4.00 Max. :165.0
## NA's :14
B1=glm(Tb ~LengthCT, family = binomial, data = Boar) # logit link is the default
summary(B1)
##
## Call:
## glm(formula = Tb ~ LengthCT, family = binomial, data = Boar)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.609 -1.120 -0.709 1.126 1.952
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -3.89211 0.67115 -5.80 6.7e-09 ***
## LengthCT 0.03161 0.00559 5.66 1.5e-08 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 700.76 on 507 degrees of freedom
## Residual deviance: 663.56 on 506 degrees of freedom
## AIC: 667.6
##
## Number of Fisher Scoring iterations: 4
plot(x=Boar$LengthCT, y = Boar$Tb,xlab="Length", ylab="Tb")
MyData=data.frame(LengthCT= seq(from = 46.5, to =165, by = 1))
Pred<- predict(B1,newdata = MyData, type = "response",se=T)
lines(MyData$LengthCT,Pred$fit,col=2,lty=2)
lines(MyData$LengthCT,Pred$fit+1.96*Pred$se.fit,col=3,lty=1)
lines(MyData$LengthCT,Pred$fit-1.96*Pred$se.fit,col=3,lty=1)

Poisson Regression
Example 1 - Poisson Regression
cfc <- data.frame(
stuecke = c(3,6,8,4,2,7,6,8,10,3,5,7,6,7,5,6,7,11,8,11,13,11,7,7,6),
attrakt = c(1,1,1,1,1,2,2,2,2,2,3,3,3,3,3,4,4,4,4,4,5,5,5,5,5)
)
attach(cfc)
plot(stuecke ~ attrakt)
fm <- glm(stuecke ~ attrakt, family=poisson)
summary(fm)
##
## Call:
## glm(formula = stuecke ~ attrakt, family = poisson)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.554 -0.728 0.037 0.591 1.546
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1.4746 0.1944 7.58 3.3e-14 ***
## attrakt 0.1479 0.0544 2.72 0.0065 **
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 25.829 on 24 degrees of freedom
## Residual deviance: 18.320 on 23 degrees of freedom
## AIC: 115.4
##
## Number of Fisher Scoring iterations: 4
newattrakt <- c(1,1.5,2,2.5,3,3.5,4,4.5,5)
preds <- predict(fm, newdata=data.frame("attrakt"=newattrakt))
lines(newattrakt, exp(preds), lwd=2, col="green")

same with 95% confidence interval:
preds <- predict(fm, newdata=data.frame("attrakt"=newattrakt), se.fit=T)
plot.new()
str(preds)
## List of 3
## $ fit : Named num [1:9] 1.62 1.7 1.77 1.84 1.92 ...
## ..- attr(*, "names")= chr [1:9] "1" "2" "3" "4" ...
## $ se.fit : Named num [1:9] 0.1459 0.1235 0.1034 0.0872 0.0775 ...
## ..- attr(*, "names")= chr [1:9] "1" "2" "3" "4" ...
## $ residual.scale: num 1
lines(newattrakt, exp(preds$fit), lwd=2, col="green")
lines(newattrakt, exp(preds$fit+2*preds$se.fit), lwd=2, col="green", lty=2)
lines(newattrakt, exp(preds$fit-2*preds$se.fit), lwd=2, col="green", lty=2)

detach(cfc)
Example 2 - Poisson Regression
Road kills data of amphibians species along a road in Portugal
load("Z:/GitHub/RMarkdowns - Stat with R/11_GLM Poisson & quasi_poisson/RK.RData")
head(RK)
## Sector X Y BufoCalamita TOT.N S.RICH OPEN.L OLIVE MONT.S
## 1 1 260181 256546 5 22 3 22.68 60.33 0.000
## 2 2 259914 256124 1 14 4 24.66 40.83 0.000
## 3 3 259672 255688 40 65 6 30.12 23.71 0.258
## 4 4 259454 255238 27 55 5 50.28 14.94 1.783
## 5 5 259307 254763 67 88 4 43.61 35.35 2.431
## 6 6 259189 254277 56 104 7 31.39 17.67 0.000
## MONT POLIC SHRUB URBAN WAT.RES L.WAT.C L.D.ROAD L.P.ROAD D.WAT.RES
## 1 0.653 4.811 0.406 7.787 0.043 0.583 3330 1.975 252.11
## 2 0.161 2.224 0.735 27.150 0.182 1.419 2587 1.761 139.57
## 3 10.918 1.946 0.474 28.086 0.453 2.005 2150 1.250 59.17
## 4 26.454 0.625 0.607 0.831 0.026 1.924 4223 0.666 277.84
## 5 11.330 0.791 0.173 2.452 0.000 2.167 2219 0.653 967.81
## 6 43.678 0.054 0.325 2.730 0.039 2.391 1006 1.309 560.00
## D.WAT.COUR D.PARK N.PATCH P.EDGE L.SDI
## 1 735.00 250.2 122 553.9 1.801
## 2 134.05 741.2 96 457.1 1.886
## 3 269.03 1240.1 67 432.4 1.930
## 4 48.75 1739.9 63 421.3 1.865
## 5 126.10 2232.1 59 407.6 1.818
## 6 344.44 2724.1 49 420.3 1.799
First plot the relationship between the distance to the closest Park and the number of road kills (TOT.N)
plot(RK$D.PARK,RK$TOT.N,xlab="Distance to park",
ylab="Road kills")

Next we fit out the Poisson GLM
M1<-glm(TOT.N~D.PARK,family=poisson,data=RK)
summary(M1)
##
## Call:
## glm(formula = TOT.N ~ D.PARK, family = poisson, data = RK)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -8.110 -1.695 -0.471 1.421 7.334
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 4.32e+00 4.32e-02 99.9 <2e-16 ***
## D.PARK -1.06e-04 4.39e-06 -24.1 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 1071.4 on 51 degrees of freedom
## Residual deviance: 390.9 on 50 degrees of freedom
## AIC: 634.3
##
## Number of Fisher Scoring iterations: 4
There is a log link between the mean of Y and the predictor function that ensures that fitted values are always non negative, unlike linear regression
Pseudo R-squared for Poisson GLMs
100*(M1$null.deviance-M1$deviance)/M1$null.deviance
## [1] 63.52
Null and residual deviance: 1) null and residual deviance are sort of equivalent of sum of squares and residual sum of squares 2) null deviance is the residual deviance in the only-intercept model, e.g the worst possible model
Plotting the fitted values
MyData=data.frame(D.PARK=seq(from=0,to=25000,by=1000))
G<-predict(M1,newdata=MyData,type="link",se=T)
F<-exp(G$fit)
FSEUP<-exp(G$fit+1.96*G$se.fit)
FSELOW<-exp(G$fit-1.96*G$se.fit)
plot(RK$D.PARK,RK$TOT.N,xlab="Distance to park",
ylab="Road kills")
lines(MyData$D.PARK,F,lty=1)
lines(MyData$D.PARK,FSEUP,lty=2)
lines(MyData$D.PARK,FSELOW,lty=2)

Back to the summary
summary(M1)
##
## Call:
## glm(formula = TOT.N ~ D.PARK, family = poisson, data = RK)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -8.110 -1.695 -0.471 1.421 7.334
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 4.32e+00 4.32e-02 99.9 <2e-16 ***
## D.PARK -1.06e-04 4.39e-06 -24.1 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 1071.4 on 51 degrees of freedom
## Residual deviance: 390.9 on 50 degrees of freedom
## AIC: 634.3
##
## Number of Fisher Scoring iterations: 4
Remember that the potential problem with Poisson GLMs is overdispersion Overdispersion means that the variance is LARGER than the mean (when we compare what we could expect from a poisson distribution)
There are 3 options to check for overdispersion: 1) Residual Deviance / degrees of freedom
M1$deviance/M1$df.residual
## [1] 7.818
Model clearly over-dispersed, it is 7.8 when it should be 1
2) 1-pchisq(residual deviance,df)
1-pchisq(M1$deviance,M1$df.residual)
## [1] 0
Model overdispersed
3)In the R package AER we can find the function dispersiontest, which implements a Test for Overdispersion by Cameron & Trivedi (1990)
library(AER)
## Warning: package 'AER' was built under R version 3.0.3
## Loading required package: car
## Warning: package 'car' was built under R version 3.0.3
##
## Attaching package: 'car'
##
## Das folgende Objekt ist maskiert from 'package:effects':
##
## Prestige
##
## Loading required package: lmtest
## Warning: package 'lmtest' was built under R version 3.0.3
## Loading required package: zoo
## Warning: package 'zoo' was built under R version 3.0.3
##
## Attaching package: 'zoo'
##
## Die folgenden Objekte sind maskiert from 'package:base':
##
## as.Date, as.Date.numeric
##
## Loading required package: sandwich
## Warning: package 'sandwich' was built under R version 3.0.3
## Loading required package: survival
## Loading required package: splines
dispersiontest(M1,trafo=1)
##
## Overdispersion test
##
## data: M1
## z = 3.219, p-value = 0.0006423
## alternative hypothesis: true alpha is greater than 0
## sample estimates:
## alpha
## 6.366
Model clearly over-dispersed, alfa should be 0
There 2 ways to solve this: 1) By running a quasi-Poisson model 2) Moving to the next level with a Negative-Binomial model
Quasi-Poisson model: Sometimes spread in count data is larger than what is possible to be modelled with a POISSON distribution It is possible to introduce a dispersion parameter p [p > 1 allows more spread than the standard Poisson mean-variance relationship (overdispersion); on the other hand, p < 1 means underdispersion] The estimation of a Poisson regression model with a dispersion parameter p is called quasi-likelihood (or quasi-Poisson), technically is no longer a poisson model. As we introduce a dispersion parameter p, all SEs are multiplied with the square root of p.
M2<-glm(TOT.N~D.PARK,family=quasipoisson,data=RK)
This is not a quasipoisson distribution (it does not exist) This is a Poisson corrected for overdispersion, a quasi-GLM model
summary(M2)
##
## Call:
## glm(formula = TOT.N ~ D.PARK, family = quasipoisson, data = RK)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -8.110 -1.695 -0.471 1.421 7.334
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4.32e+00 1.19e-01 36.16 < 2e-16 ***
## D.PARK -1.06e-04 1.21e-05 -8.73 1.2e-11 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for quasipoisson family taken to be 7.63)
##
## Null deviance: 1071.4 on 51 degrees of freedom
## Residual deviance: 390.9 on 50 degrees of freedom
## AIC: NA
##
## Number of Fisher Scoring iterations: 4
Plot the predictions one more time but this time corrected for overdispersion
MyData=data.frame(D.PARK=seq(from=0,to=25000,by=1000))
G<-predict(M2,newdata=MyData,type="link",se=T)
F<-exp(G$fit)
FSEUP<-exp(G$fit+1.96*G$se.fit)
FSELOW<-exp(G$fit-1.96*G$se.fit)
plot(RK$D.PARK,RK$TOT.N,xlab="Distance to park",
ylab="Road kills")
lines(MyData$D.PARK,F,lty=1,col=2,lwd=4)
lines(MyData$D.PARK,FSEUP,lty=2,col=2)
lines(MyData$D.PARK,FSELOW,lty=2,col=2)
 When comparing this model predictions (where we deal with overdispersion) with the first Poisson model, we can observe the same fitted values but completely different errors.
When comparing this model predictions (where we deal with overdispersion) with the first Poisson model, we can observe the same fitted values but completely different errors.
Technical details
## Poisson with optimization by hand
# data
cfc <- data.frame(
stuecke = c(3,6,8,4,2,7,6,8,10,3,5,7,6,7,5,6,7,11,8,11,13,11,7,7,6),
attrakt = c(1,1,1,1,1,2,2,2,2,2,3,3,3,3,3,4,4,4,4,4,5,5,5,5,5)
)
attach(cfc)
plot(stuecke ~ attrakt)

# defining the likelihood of a Poisson regression
loglikelihood <- function(par, independent = attrakt, observed = stuecke){
linear = par[1]*independent + par[2] # linear predictor
predict = exp(linear) # link function
logprobabilities = dpois(observed, predict, log=T) # distribution
return(-sum(logprobabilities))
}
# plotting the likelihood for different slopes, fixed intercept
slope=seq(0.05,0.25,length.out = 100)
intercept = rep(1.4,100)
pars = cbind(slope, intercept)
plot(slope, apply(pars,1, loglikelihood), main = "Likelihood profile", ylab = "Neg Log Likelihood")

# plotting the likelihood surface (= likelihood as a function of slope, intercept)
intercept = seq(1.2,1.7,length.out = 100)
parametervalues = expand.grid(slope,intercept)
parametervalues$response = apply(parametervalues,1, loglikelihood)
contour(slope, intercept, matrix(parametervalues$response, nrow = 100), nlevels = 20, main = "Likelihood response surface", xlab = "slope parameter", ylab = "intercept parameter")
# optimization with the optim function
bestfit = optim(c(0.12,1.3), loglikelihood, method = "BFGS")
points(bestfit$par[1], bestfit$par[2], col = "red", lwd = 4)

# calculating the "Hessian" matrix (Funktionaldeterminante)
bestfit = optim(c(0.12,1.3), loglikelihood, method = "BFGS", hessian = T)
bestfit$hessian
## [,1] [,2]
## [1,] 2225 573
## [2,] 573 174
persp(slope, intercept, matrix(parametervalues$response, nrow = 100), theta = 40, phi = 30, expand = 0.7, col = c("grey","red"), ticktype = "detailed")

# bonus plot
library(rgl)
## Warning: package 'rgl' was built under R version 3.0.3
##
## Attaching package: 'rgl'
##
## Das folgende Objekt ist maskiert from 'package:car':
##
## identify3d
persp3d(slope, intercept, matrix(parametervalues$response, nrow = 100), col = c("grey","red"), box = FALSE)
detach(cfc)
Links
http://blog.revolutionanalytics.com/2014/04/some-r-resources-for-glms.html